循环神经网络(RNN)让神经网络有了记忆,能够更好的模拟序列化的数据。虽然RNN的原理很简单,但代码特别是参数上,需要花一些时间去理解。以下我们用Pytorch中的RNN类,实现用sin曲线预测cos曲线的模型。
代码示例
1、生成数据集
仅演示效果,和模型逻辑无关
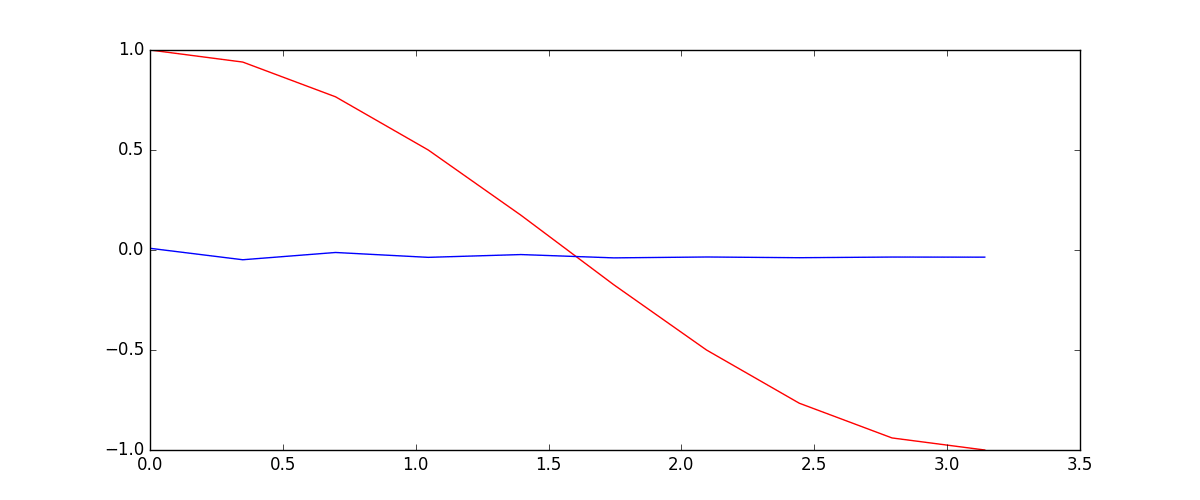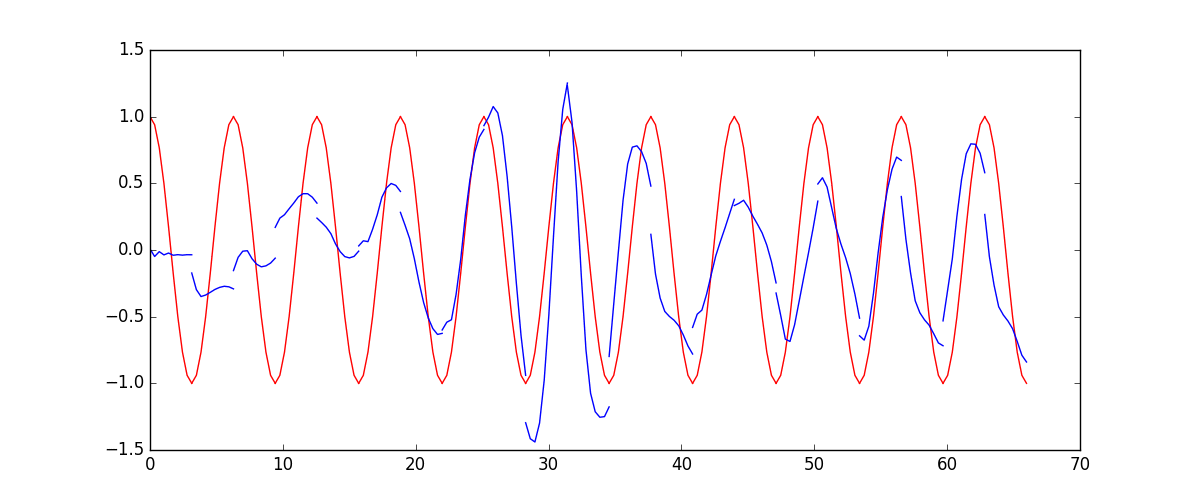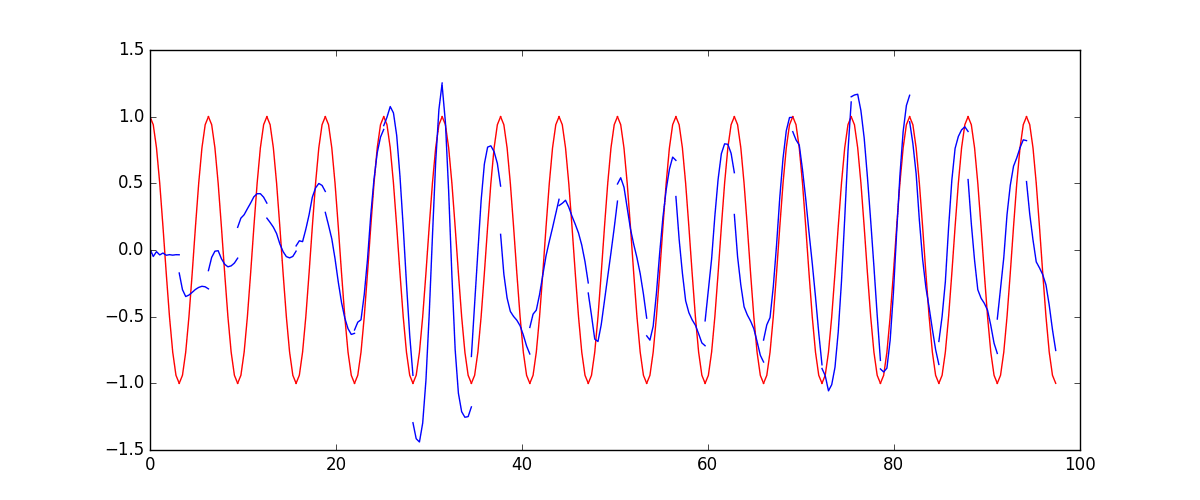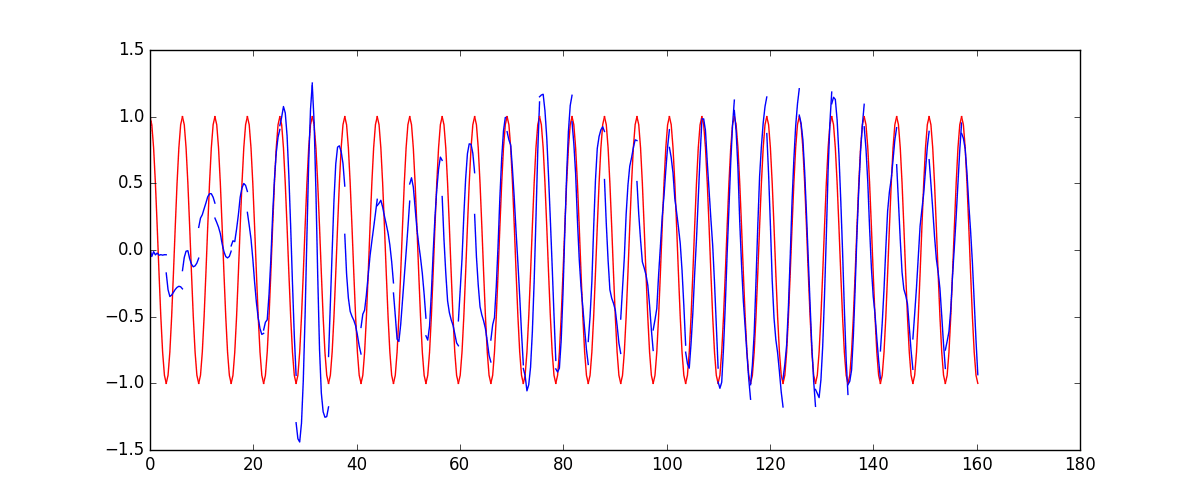
import numpy as np import matplotlib.pyplot as plt steps = np.linspace(0, 2*np.pi, 100, dtype=np.float32) x_np = np.sin(steps) y_np = np.cos(steps) plt.plot(steps, x_np, 'b-', label='input (sin)') plt.plot(steps, y_np, 'r-', label='target (cos)') plt.legend() plt.show()
2、定义模型
import torch.nn as nn
class Net(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=hidden_size,
batch_first=True,
)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x, h_state):
outs, h_state = self.rnn(x, h_state)
# 用10个输出,拟合10个目标点
return self.fc(outs), h_state
3、参数定义和模型实例化
import numpy as np import torch input_size = 1 output_size = 1 time_step = 10 hidden_size = 32 net = Net(input_size, hidden_size, output_size)
4、模型训练
epoch = 100
loss_fn = nn.MSELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.02)
plt.figure(figsize=(20, 4))
plt.ion()
h_state = None
for i in range(epoch):
steps = np.linspace(i * np.pi, (i + 1) * np.pi, time_step, dtype=np.float32)
x_np = np.sin(steps)
y_np = np.cos(steps)
x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])
y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])
y_pred, h_state = net(x, h_state)
# 也可以用 h_state = h_state.detach()
h_state = h_state.data
loss = loss_fn(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 模型可视化
plt.plot(steps, y_np, 'b-')
plt.plot(steps, y_pred.data.numpy().flatten(), 'r-')
plt.draw(); plt.pause(0.05)
plt.ioff()
plt.show()
这个例子虽然是回归场景,但预测的也是一个曲线,RNN中每次输出值都压入了预测值,不是常规的回归任务,不是很好理解。
本文为 陈华 原创,欢迎转载,但请注明出处:http://www.chenhuax.com/read/302



